By Dr. Alec MacAndrew, 22 August 2014
“J’ai toujours aimé la vérité avec tant de passion, que souvent j’ai commencé par mentir afin de parvenir à la faire entrer dans des têtes qui n’en connaissaient pas les charmes.” — Giacomo Casanova
Imagine that you are an enthusiastic supporter of some aspect of science that runs counter to the mainstream. Suppose that you have been challenged to explain a key observation using your scientific hypothesis, which is at variance with that of the mainstream. You are a Christian who wears your religion on your sleeve. You are proud to proclaim that your hypothesis is informed by your religious beliefs, and while you are adamant that your religious beliefs trump the claims of secular science, you also declare that there can be no contradiction between your interpretation of Christianity and true science. You therefore propose to answer the challenge scientifically. You expend the time and effort because you want to change hearts and minds and win thinking people over to your point of view by showing how your idea explains the evidence. You might even have an ambition to appeal to scientists and to put a case that, in time, would replace the currently accepted scientific paradigm.
Imagine yourself in this situation – how would you set about doing this and what things would you avoid? Well, first of all, you would make sure that the alternative scientific explanation that you propose would be sufficiently different from the mainstream approach to distinguish between the two. You would make sure that your explanation uniquely supports the fundamental hypothesis that you are promoting. To avoid being dismissed as an incompetent crackpot, you would make sure that your work is internally consistent and free from errors, and especially free from elementary mathematical blunders. As a 
Christian, showing an example to the world, you would be extra careful to ensure that you argue ethically, not just because that’s important to your credibility, but because it’s the right thing to do. You would, wouldn’t you?
Well, Dr Gerardus Bouw has failed on every front. His article “A Geocentric Solution to the Three Body Problem” was posted on Mr Sungenis’s website here (accessed 22 August 2014). Dr Bouw sets out his stall right from the beginning:
…Bob Sungenis invited me to derive a geocentric solution within the framework of the theory of geocentricity. Our purpose was to derive a viable geocentric framework for the 3-body problem. We were successful and this paper is the fruit of our labors.
Dr Bouw proposes to derive the positions of the five Sun-Earth Lagrange points using geocentric theory. The Lagrange points are places where, assuming that there are two bodies orbiting their common centre of mass, a third body of negligible mass will orbit stably with the same period. This is known as the restricted three body problem (‘restricted’ because the solutions are valid only for cases where the third body has a negligible mass compared to the other two and some other conditions are fulfilled). Dr Bouw is proud, even boastful about his achievement:
Unlike most modern dynamic derivations posted on the web which know the solutions ahead of time, the approach in this paper is completely general and so could be used to locate any additional critical points besides the five Lagrangian points.
So what does Bouw’s paper contain? Although it is quite lengthy, there are just three major sections:
- The first section attempts to show, using Newtonian mechanics, that there are forces available in the geocentric case to keep all the astronomical bodies in the universe rotating about the Earth once per day (and that there is a force that maintains astronomical bodies at whatever angle above or below the Earth’s equator they happen to occupy). This derivation contains elementary mathematical blunders. When those errors are corrected the derivation gives the vast centripetal force that would be required to maintain a star or galaxy in a daily orbit round the Earth, but proposes no source for that force.
- The second section is a complex analysis of the restricted three body problem, including the derivation of the positions of the Lagrange points, occupying 18 pages of mathematics and diagrams in Bouw’s article, totally plagiarised unreferenced from an early 20th Century textbook (An Introduction to Celestial Mechanics, by Forest Ray Moulton, The MacMillan Company New York, Second Revised Edition, 1914, pages 277 – 294), Open Library Cat number: OL7106592M)
- The third section of five pages is a more modern derivation of the positions of the Lagrange points, copied wholesale and word for word from a modern tutorial by Dr Neil Cornish, “The Lagrange Points“. Part of the same Neil Cornish tutorial was plagiarised in a previous article written by Sungenis here. That article is also riddled with a range of scientific and mathematical errors. In this case, Bouw does reference Cornish, but as I have pointed out elsewhere, it is very dubious practice to copy multiple pages of others’ work whether or not you reference them. Using short quotations is fair use – exact reproductions of complete sections is not.
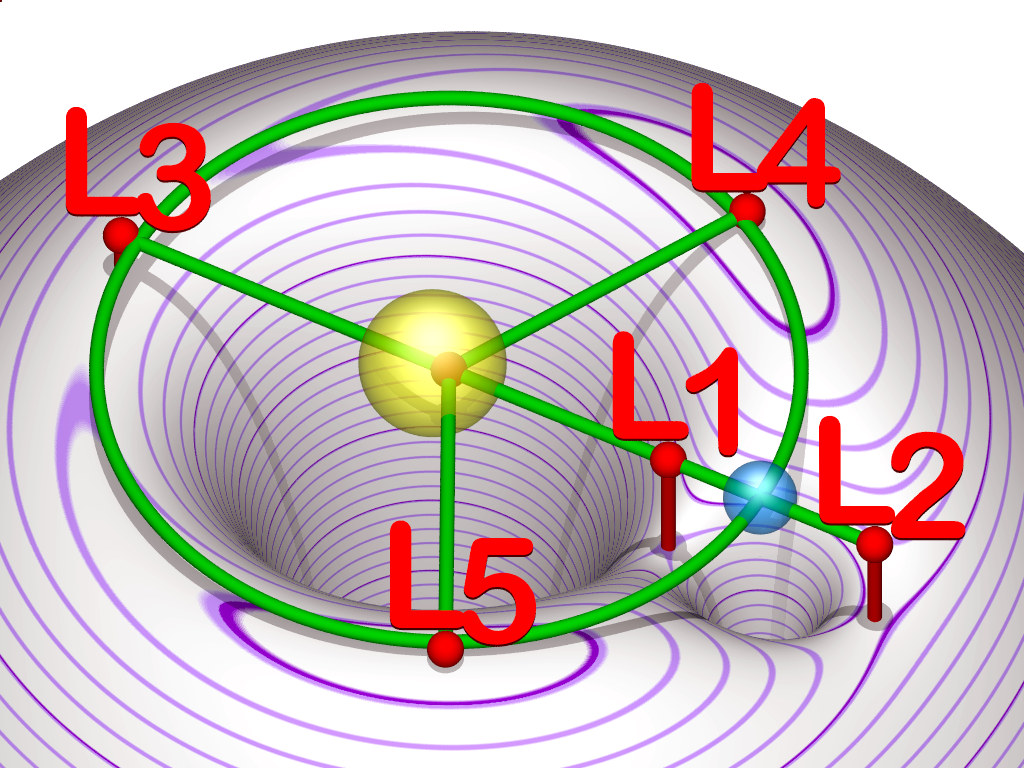So, what have we got here? Has Bouw made good on his boast to derive a viable geocentric framework for the three-body problem? Well, we have an analysis of the forces that would be required to keep stars and galaxies rotating daily about the earth but no source for those forces. That derivation contains elementary mathematical blunders and so gives an incorrect expression for the force required. We also have two lengthy mainstream derivations of the positions of the Lagrange points written by other people, which occupy 23 of the 30 pages of Bouw’s paper, one of which Bouw has plagiarised without reference or acknowledgement and the other of which is an exact copy of the original. These derivations are based on Newtonian mechanics in which the Sun and Earth orbit their mutual centre of mass and in which the Earth is not static. That’s it. That’s all he’s got. All we get is mathematical and scientific incompetence, intellectual theft and an abject failure to achieve the declared objectives.
Now, let’s look at the three sections in a little more detail.
Section 1 – Bouw’s incorrect derivation of the force on a star rotating about the earth’s axis daily
The mathematics in the first section, in which Bouw purports to calculate the forces associated with a universe that rotates daily around a static Earth, is almost but not quite identical to a section in this Sungenis paper. The maths in both these articles contains elementary mathematical blunders, some common to both, some different. My analysis below refers to the current article. (But see here for my critique of the multiple errors in the similar section of the earlier article.)
Bouw’s definition of terms and his notation are very poor. For example he defines R as “the shortest distance from the axis of rotation to the star”. A distance is a scalar quantity that has magnitude but no direction, but Bouw uses R as a vector quantity which has magnitude and direction. So, R should correctly be defined as the displacement of the star from the axis, a vector which rotates around the axis with the star. When doing linear algebra, a number of conventions are available for distinguishing between vector and scalar quantities – for example making vector symbols bold or putting an arrow accent on them or underlining them to distinguish them from scalars. It doesn’t much matter which convention is used, but for clarity, you should use one and stick to it, because the algebraic rules for vectors and scalars are different and because vectors and scalars have different physical meanings. Bouw uses the bold convention in a couple of places, but mostly doesn’t use any. However, since most of the maths (up to the key error I describe below) is merely the routine textbook derivation of the acceleration and force relating to a body moving in a rotating frame, it’s relatively straightforward for someone already familiar with this derivation to figure out which quantities are meant to be vectors. Nevertheless, the erroneous definitions and the ambiguous mathematical notation are evidence that he doesn’t really understand what he’s doing.
Since the vector v, the velocity of the star referred to the rotating frame, is zero (the star rotates with the same angular velocity as the rotating frame), you can get to Bouw’s equation 9 much more readily than he does, but nevertheless his equation 9 is correct. Equation 10 is the correct scalar product expansion of the vector triple product in equation 9. Then Bouw goes badly wrong. He writes:
Now the star is not located on the equator but at declination δ, whence ω.R = D ω sin(δ)
This is completely, hopelessly and naïvely wrong. R and ω are orthogonal vectors, i.e. vectors at right angles to one another. (By Bouw’s own definition, the direction of R is at right angles to the Earth’s polar axis and the direction of ω is along the Earth’s polar axis.) The scalar or dot product of two orthogonal vectors is zero – this is an elementary identity in vector algebra. The first term in Bouw’s equation 10 should therefore be zero yielding the correct answer from the non-zero second term: a = ‑ω2R, as I have pointed out on two previous occasions. These guys aren’t just wrong but incorrigibly wrong. The term in their equation 11, ω2 (D sinδ), is entirely spurious – there should be no term in the acceleration which is parallel to the polar axis (you can see that this must be so by casual inspection of equation 9: a = ω x (ω x R) which shows, since ω and R are orthogonal, that the acceleration must be antiparallel to R with no component along the polar axis). Their goof propagates through to their equation 12, the culmination of their derivation, rendering it just wrong. The bungling incompetence of Bouw’s elementary vector algebra is remarkable, especially for someone claiming to develop a new theory of celestial mechanics in order to revolutionise our understanding of physics.
The force required to accelerate the star around a circular orbit once per day is given by F = ma = ‑mω2R, where m is the mass of the star. I have previously calculated what that force and acceleration might be for a solar mass star located at, say, redshift z=0.1 away from the Earth’s polar axis and revolving around it once per day. The distance of the star from the polar axis is 1.3×109 light years, which is 1.23×1025 metres. The angular velocity is 2π radians per day or 7.3×10-5 radians per second. The centripetal acceleration required is then 6.6×1016 ms-2 or 6.7 thousand trillion times the acceleration due to gravity at the Earth’s surface. The centripetal force required to accelerate a solar mass star of 1.98×1030kg thus would be 1.3 x1047 Newtons which is a truly stupendous force. Needless to say, there is no source for such a vast force acting on the star and pointing at the earth’s polar axis.
So this first section of Bouw’s work contains basic errors, draws unwarranted conclusions and fails to support his thesis.
Section 2 – Plagiarism of F R Moulton’s 1914 textbook
Forest Ray Moulton’s hundred year-old textbook contains a rather old-fashioned derivation of the positions of the Lagrange points. He starts from first principles by writing down the Newtonian equations of motion for the three bodies (in our case Sun, Earth and an infinitesimally light test particle) and then derives the surfaces of relative zero velocity of the infinitesimal body using rigorous methods. The entire section that is plagiarised by Bouw occupies 18 pages of quite dense mathematics in the original (the maths although dense, is relatively straightforward, consisting mainly of classical algebra and classical differential geometry). Bouw copies the entire 18 pages. He copies the mathematical expressions exactly using identical notation to the original. In some cases he paraphrases the text between the mathematical expressions, in others he copies it word for word, but in every case the import of his text is identical to the original. A typical example is:
Moulton (the original): Since only the squares of y and z occur, the surfaces defined by (8) are symmetrical with respect to the xy and xz-planes, and, when μ =½, with respect to the yz-plane also. The surfaces for μ ≠ ½ can be regarded as deformations of those for μ = ½. It follows from the way in which z enters that a line parallel to the z-axis pierces the surfaces in two (or no) real points. Moreover, the surfaces are contained within a cylinder whose axis is the z-axis and whose radius is √C , to which certain of the folds are asymptotic at z2 = ∞; for as z2 increases, the equation approaches as a limit: [page 282]
Bouw (as plagiarised from Moulton): Since only the squares of y and z occur, the surfaces defined by (21) are symmetrical with respect to the xy and xz-planes, and, for the case that μ = 0.5, with respect to the yz-plane also. The surfaces for μ ≠ 0.5 can be regarded as deformations of those for μ = 0.5. From the geometry of z it follows that a line parallel to the z-axis pierces the surfaces in two or none real points. Also, the surfaces are contained within a cylinder whose axis is parallel to the z-axis and whose radius is √C , to which certain folds are asymptotic at z2 = ∞; for, as z2 increases, the equation approaches as a limit: [page 11]
He conducts this sort of close paraphrasing for 18 pages, interspersed by the exactly copied mathematical expressions. Bouw also copies the diagrams from Moulton’s book exactly – they appear to be scanned from the original. Amazingly, Bouw has gone to the trouble, not just here but with the Cornish paper discussed below, of transcribing, in identical form to the original, all the many complex equations, using LaTex or some other Equation Editor. That labour of deception must have been dismally tedious. (He makes a few transcription errors that we needn’t worry about).
What in heavens is going on here? Did Bouw really expect people to believe that he had developed this derivation himself? Could he possibly think that? He must have done, for he introduces this section by writing:
There remains for us to derive the generalized equations of motion describing the path of the test mass, m. Then we need to solve the generalized equations for locations where m’s velocity is zero relative to both sun and earth. [My bolding]
It takes only a cursory inspection to see that the diagrams are in an out-moded style, that the mathematical notation is old-fashioned and that there are technical terms that few would use today (for example talking about the “right member” of an equation where most today would say the “right-hand side”, an anachronism that Bouw repeats). It is immediately obvious that this is copied from an older source and it didn’t take me long to find Moulton’s original book in Google Books and to find a complete copy of the book on-line in the Open Library.
This is a double failure for Bouw and for geocentrism. Their so-called “successful” derivation of a “viable geocentric framework for the three body problem” turns out to be nothing more than the dishonest counterfeit of a classical Newtonian derivation which is based on equations of motion in which the Earth and Sun orbit their mutual centre of mass (and so which is clearly not geocentric). Not only does the derivation not do what he claims for it, but his reputation for honesty, such as it was, is in tatters.
Section 3 – Copying a modern derivation – Neil Cornish’s work
What is it about promoting geocentrism that persistently leads people into the plagiarism and copying of others’ work? I have already pointed out that part of Neil Cornish’s tutorial was plagiarised in an earlier Sungenis article. At the date of writing, Sungenis has done nothing to attribute the Cornish work properly or to apologize for stealing from it. In that same article, Sungenis presented some of Dr Luka Popov’s work unreferenced and as if it was his own. In his article on the BICEP2 announcement here, he reproduces pages and pages of others’ work, which, although he does reference the original authors (in some cases unclearly), is dubious practice and possible breach of copyright.
Bouw’s use of Neil Cornish’s derivation of the Lagrange points falls into this last category – five pages or so, copied word for word, diagram for diagram and equation for equation. He references the Cornish original paper in a footnote to his section title but introduces this section thus:
In this section, we use another approach which is based on Newtonian gravitational force. We again start with the same initial conditions as we did with Figure 4, here presented as Figure 10. [My bolding]
The first paragraph of this section on p26 and the two concluding paragraphs on p30 are written by Bouw, and everything in between is an exact copy of Cornish’s paper. Bouw does nothing to distinguish between his words and Cornish’s – no quotation marks, no italics, no indentation. The fact that he gives a reference in this case is hardly sufficient to avoid plagiarism and does nothing to avoid breach of copyright. It’s possible that Bouw got permission from Dr Cornish to copy a large part of his article, but that seems unlikely. But even if he did, the way it is reproduced, with Bouw’s work and Cornish’s work presented indistinguishably, is unacceptable.
Just as in the previous section, this section of Bouw’s paper fails to promote the geocentric case. Cornish’s approach is somewhat different from Moulton’s, relying on gravitational potential considerations rather than the equations of motion. The result is more restricted in application but is still entirely standard mainstream physics in which the Earth orbits the centre of mass of the Sun-Earth system and is not static. As with Moulton, there is nothing especially geocentric about it.
To conclude
Bouw’s trumpeted geocentric derivation boils down to the dishonest copying of two mainstream solutions to the problem.
It will be interesting to see whether, after this critique, the Bouw article is silently corrected or whether it disappears altogether. The ethical thing for Bouw and Sungenis to do would be to … well, what do you think is the ethical thing that Bouw and Sungenis should do in the light of the facts presented here?
The geocentrists’ grand announcement “Our purpose was to derive a viable geocentric framework for the 3-body problem. We were successful and this paper is the fruit of our labors” has turned to ash in their mouths. The challenge to the geocentrists to derive the positions of the Lagrange points using a geocentric framework remains outstanding.
