Aether, Springs, and Light: Physics Blunders in Galileo Was Wrong

by Dr. Alec MacAndrew

1 Introduction

I sometimes browse Mr Robert Sungenis’s Facebook page here, the one called Ask Robert Sungenis about Geocentrism, because the spectacle of a man virtually devoid of education in science giving absurd answers to earnest scientific questions posed by his undiscerning admirers can be very funny.

As it is on the Facebook page here, where Sungenis answered a question about the propagation of light in a “rotating universe”. There is much wrong with his reply, which we’ll get to later, but one very elementary mistake jumped out at me. His reply depends on the existence of a speculative medium, the “geocentric aether”, which he invented and which he believes is needed for the propagation of light. He claimed, among other things, that the speed of light depends on the tension in the aether (don’t worry, we’ll come back later to these claims about how light travels) and he provided an analogy for how he thinks this works.

The analogy he chose is a spring in tension and he gave an expression for the speed of waves along such a spring. His expression is v = T/μ^-2 (T is the tension and μ is the mass per unit length of the spring). This is hopelessly wrong – the correct expression is v = √(T/μ). Also, the expression T/μ^– 2 is bizarre because it is mathematically awkward – one would usually write it Tμ² (but perhaps he meant (T/μ)^-2, which, although less awkward mathematically, is still wrong so far as the physics goes). Further on, Sungenis claimed that if the tension is 100 times greater, the speed would be “100^– 2 or 10 times greater”. This is grotesquely wrong because 100^-2 is another way of writing 1/100² which is 1/10,000 which equals 0.0001. 100^-2 is not 10 – it’s not even close. He is out by a factor of 100,000. What’s going on here?

I realised that most of his answer was based very closely on a section in his book, Galileo Was Wrong[1] (GWW) where he used the correct expression for the speed of the wave in a tensioned spring.[2] Then it dawned on me that Sungenis, in transcribing the contents of GWW to the Facebook com-box, had been forced to use exponential notation because the symbol, ‘√’, representing a square root is not available in Facebook comments. Fair enough.

But unbelievably, shamefully, he knows so little about arithmetic notation, indeed far less than a good high-school pupil does, that he thinks x ^-2 means the square root of x. Not true – of course x ^-2 doesn’t mean the square root of x – it means 1/x², the reciprocal of the square of x. The square root of x, written in exponential notation is, of course, x^1/2, and so the things he should have written were v = (T/μ)^1/2 and 100^1/2 (rather than what he did write, v = T/μ^-2 and 100^-2; the differences are profound). This ought to be within the compass of anyone who has benefitted from a modest general education and yet it is beyond him. This is a man who would overthrow the worlds of physics, astronomy and cosmology – I find it absurd and dispiriting that his vaulting ambition should so overstep his meagre ability. And not one of his followers on the Ask Robert Facebook page picked him up on this latest blunder which we can now add to his long and dismal list of incompetent mistakes.

But this boogaloo is all by way of preamble. Having been led to this section in GWW, I noticed he makes other claims there about the geocentric aether in which he gets the physics exactly backwards, and that is what this article is really all about.

2 Sungenis’s imaginary friend

What is this Planck-aether medium of geocentrism that Sungenis bangs on about?[3] Well, he isn’t very clear about it himself, except that its properties are always exactly what he needs them to be in support of geocentrism. He certainly isn’t at all clear about how his Planck-aether can be detected (it hasn’t been, either directly or indirectly), nor how we can know of its existence and measure its properties (the properties can’t be measured, because the thing itself has not been detected).

However, we can infer something about his proposition from his description:

In the geocentric system, a diurnally rotating universe creates tremendous centrifugal forces which, according to Einstein’s own covariance equations, are equivalent to the force of gravity. As such, light traveling in this kind of superdynamic environment can greatly exceed 3 × 10^8 m/sec. As Rosser notes “light can assume any numerical value depending on the strength of the…centrifugal gravitational field” which has “enormous values at large distances.” In the Planck-ether medium of geocentrism, the speed of a transverse wave, such as light, depends on the tension between the Planck particles. [His emphasis and his ellipsis]

The Planck-aether medium of geocentrism is Sungenis’s own invention that consists of a solid plenum of Planck particles, which are highly speculative hypothetical entities that have not been detected either directly or indirectly.[4] The uniform density of Planck particles would be 4.9 x 10⁹¹ g/cm³. Such a density would mean that the mass of Sungenis’s aether in one cubic centimetre is a stupendous factor of 10³⁶ more than the ordinary mass in the entire observable universe. There is no known physical phenomenon which depends on their existence.

Note that Sungenis’s Planck-aether is neither the long-abandoned classical luminiferous aether, nor the energy of the vacuum, neither of which have properties anything like that claimed by Sungenis for his Planck-aether.

Working physicists don’t think that Planck particles or a solid aether made of them actually exist. Indeed, the mass-energy density of space is measured to be about 10^-29 g/cm³ (about 5 hydrogen atoms per cubic metre), or about 10¹⁰⁹ times less than Sungenis’s Planck-aether – direct observational evidence that it doesn’t exist. It’s a complete fantasy.

Sungenis faces another difficulty: If his Planck-aether is rotating about the Earth, it would be rotating not about the Earth as a point, but about Earth’s polar axis which extends indefinitely away from the Earth into space from the North and South poles. The “centrifugal gravitational field” in a rotating universe does not have “enormous values at large distances” on the axis of rotation – in fact, it is zero, no matter how far away from the Earth you go.[5] So according to Sungenis’s own idea, the speed of light at great distances from the Earth along the polar axis would be the same as it is locally on Earth but it would be hugely greater at great distances on the equatorial plane. This idea is negated by observations, and it violates general covariance. It’s a fantasy.

Sungenis asserts confidently that his invented Planck-aether can “sustain” (whatever that means) “millions of orders of magnitude” greater tension than its tension at the Earth (note: not merely a factor of millions, but millions of orders of magnitude!), that it is “incompressible” at the Earth, that it can be stretched to “great dimensions” and “remain stable”, but that it is “strong” and would take a “tremendous amount of centrifugal force to stretch it”. His aether has “such high granularity” (whatever that means) that it doesn’t “react with baryonic matter” but with “electromagnetic and gravitational activity” (see GWW, Vol 1, page 263).[6] How can he possibly know these things? His claims are vague, unquantified and entirely unsatisfactory to physicists, they arise without rhyme or reason, and he never explains how he has come by them. Their empirical and mathematical foundation remains a mystery. The undeniable fact is that he’s just making it up. His kind of knowledge is like that of a child who just knows her imaginary friend is wearing a blue dress and has brown eyes. It’s a fantasy.

But let’s indulge the fantasy for a while. Let’s temporarily suspend our disbelief and grant Sungenis his aether for a time. Let’s step into his invented world and see whether, even if it existed, it would behave the way he says it would.

3 Twirling the spring

Sungenis uses the analogy of a spring representing his Planck-aether to explain how, in his model, in which the Universe rotates around the Earth, light travels faster the further from the Earth you get. He says:

In the Planck-ether medium of geocentrism, the speed of a transverse wave, such as light, depends on the tension between the Planck particles. The greater the centrifugal force, the greater the tension and thus the greater the speed of light. The inertial force of a rotating universe increases as the distance from the center of mass increases. Consequently, the farther from Earth a star is in a rotating universe, the faster its light can travel toward Earth, the center of the universe. By the time the light reaches the environs of Earth, however, it will be traveling at the minimum speed of 3 × 10⁸ m/sec since the surface of the Earth is at or near the neutral point of the centrifugal force created in a rotating universe. Outside of this locale, light can travel at much greater speeds than 3 × 10⁸ m/sec. Since that is the case, we may be looking at the explosion of supernovae precisely when they occur in deep space.

We shall not be distracted by Sungenis’s last rhetorical sleight of hand, where he asserts that we could be seeing “supernovae precisely when they occur in deep space”, a prediction which is trivially and obviously wrong for any finite speed of light. Let’s focus on his idea that if the universe is whirling around, the tension in his hypothesised aether is greater as a function of distance owing to centrifugal force, and that the greater tension with distance results in a higher speed of light according to the formula we have seen already, v = √(T/μ). He continues his exposition by comparing the Planck-aether to a spring:

We can grasp this phenomenon intuitively by illustrating the stretching of a metal spring. If we hit the end of an unstretched spring, the vibration will travel to the other end of the spring in a certain time and velocity. If we stretch the spring to about three times its original length, the vibration will travel proportionately faster due to the increased tension in the spring. Likewise, if we whirl the spring around in a circle, the centrifugal force stretches the spring. Similarly, a rotating universe stretches the ether medium within it. The greater the radius of the rotation, the greater the centrifugal force, and thus the greater the tension in the ether medium. This will result in a greater speed for light traveling through that medium.[7]

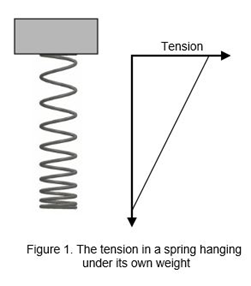
Before we consider the whirling spring as an analogy for the whirling aether, let’s limber up our thinking muscles by considering a related but simpler case – a spring under tension and extended only by its own weight. In that case, the tension in the spring varies along its length. The greatest tension occurs at the top fixed point of the spring because the entire weight of the spring has to be supported at this point. The least tension, in fact zero tension, occurs at the very bottom end of the spring where there is no mass below to be supported, so there is no tension in the spring at this point (see Fig. 1). Let’s imagine that the spring is a long chain of people, dangling head-down under gravity, holding, desperately for fear of precipitate disaster, on to each other’s feet, with the feet of the guy at the top attached to a rigid platform. The tension in the ankles of the bottom dangler is his own weight – the tension in the ankles of the one at the top is his own weight plus the weight of all the others hanging below him. He’d better be the strongest of them all if they are not to plummet to their deaths. In a similar way it is clear that, for a spring hanging under its own weight, the greatest tension (and extension) is at the top next to the fixed point and the least tension (and extension) is right at the bottom at the free end. So the velocity of a transverse wave will vary along such a spring, being greatest at the top and falling to zero at the bottom.[8]

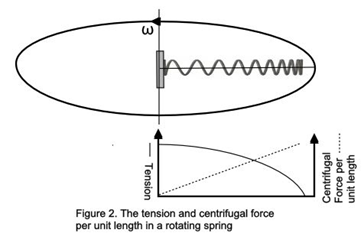
OK, let’s get a little more complicated and explore what happens when we whirl the spring horizontally around a fixed point. Gravity is no longer relevant but centrifugal force is. Sungenis says:

The greater the radius of the rotation, the greater the centrifugal force, and thus the greater the tension in the aether medium

This is how Sungenis concludes that the speed of light is greater away from the Earth. Is his argument correct? No. In fact, Sungenis has it exactly backwards. It’s true that the case of the whirling spring is a little more complicated than that of the hanging spring. The force exerted by gravity on any element of the hanging spring is the same as every other (it’s just the mass of the element times the acceleration due to gravity), but in the whirling case it also depends on the radial distance of the element from the centre (it’s the mass of the element times its distance from the centre times the square of the angular speed of rotation). However – and this is the important point – the principle, which we have already explored for the hanging case, that the tension is greatest in the centre remains true for the rotating case. An element at the centre, although not experiencing a centrifugal force arising from its own rotation, has the outward force exerted by the entire spring pulling on it, whereas an element at the far end has none of the spring beyond it, no external force to pull on it other than the centrifugal force of its own rotation, and so it is not in tension. The centrifugal force acting along the spring is greatest at the end and zero in the centre, but the tension in the spring is greatest in the centre and zero at the end.[9]

Our analogy of a chain of people works here too. What if we whirl a chain of people around? The guy at the end has no-one else’s centrifugal force to pull on him. The next person in has a smaller centrifugal force acting directly on him than the one on the end, but, in addition, he has to hold on to the feet of the person on the end and is tugged by his force. And so it goes, the strong-man in the centre has little centrifugal force acting directly on him, but has the centrifugal force of everyone else in the chain pulling on him. If he lets go, the entire chain flies off. He is physically (and psychologically) under the greatest tension.

What does this mean for Sungenis’s analogy? Well, if the Planck-aether is like a spring being whirled around then the tension will be greatest in the centre, and that is where the highest wave speed will be, where the tension is highest and the linear density is lowest, near the Earth. In fact, if his hypothesis that light is a transverse wave in the Planck-aether with a speed given by the spring-in-tension formula is correct, and that tension is caused by the centrifugal force of the rotating Planck-aether, then the speed of light would be less the further away from the Earth you go, the complete opposite and contradiction of his claim.

4 Going solid

A spring in tension is the analogy that Sungenis has chosen to represent his Planck-aether, but the physics of a spring is that of a one dimensional entity that vibrates in space. Presumably the aether, as Sungenis understands it (remember, Sungenis’s Planck-aether is a made-up fantasy, but we’re indulging it for a while), is a solid three dimensional thing, and in his mind, light is a transverse (shear) bulk wave travelling in it. So a better analogy for the Planck-aether would be a solid uniform rotating disc. Perhaps in this case, the transverse wave speed would be greater at greater radii? Sadly for Sungenis the answer is no – the greatest stress still occurs in the centre. (Stress is force per unit area and is the solid body analogue of tension – we need to consider stress rather than tension when examining the behaviour of solid bodies). This fact is well known to engineers – for example, rapidly rotating turbine blades tend to fail at the root where the stress is greatest, not at the tip.

In the case of a solid rotating disc there are two stresses to consider – radial stress which is the stress acting in a direction from the centre to the periphery and hoop stress which acts around the circumference. The derivation of these stresses in a rotating solid disc is standard physics, available in many textbooks, and the results well-known. The total stress is greatest in the centre, which is where the greatest strain will also be (strain is the distortion of the material as a result of stress). Consequently, the bulk density of the rotating disc will be least in the centre.[10]

The speed of shear bulk waves in a solid is given by v = √(m/ρ) where m is the shear modulus of the material and ρ is its bulk density. It’s obvious, that even with this better analogy for his aether, the physics gives results in exact contradiction to the way Sungenis would have it. As the stress and strain are tensile and greatest in the centre, so the density would be least there, and thus the velocity of transverse waves would be highest. So, according to this better analogy, as is the case with Sungenis’s own spring analogy, light speed would be greatest at the Earth and would be less the further away you go, exactly the opposite of his claim.

5 Returning to sanity

Our journey through Sungenis’s fantastic world has come to an end, and we must return to humdrum reality. It’s time to abandon the analogy of a whirling spring, an analogy representing the bizarre notion that light consists of transverse waves in a solid, incredibly dense Planck-aether of speculative undetectable particles. Let’s examine other ways in which his hypothesis fails.

Across much of his writing Sungenis and his supporters repeatedly fall into what I call the Great Inconsistency, appealing to the conclusions of General Relativity while vehemently rejecting them (see Here Comes the Sun, p.17, and There He Goes Again, p.2). The section from GWW that we are reviewing is no exception. He quotes W G V Rosser’s review of General Relativity approvingly in spite of the fact that he rejects the theory:

As Rosser notes “light can assume ANY NUMERICAL VALUE depending on the strength of the…centrifugal gravitational field” which has “enormous values at large distances.”

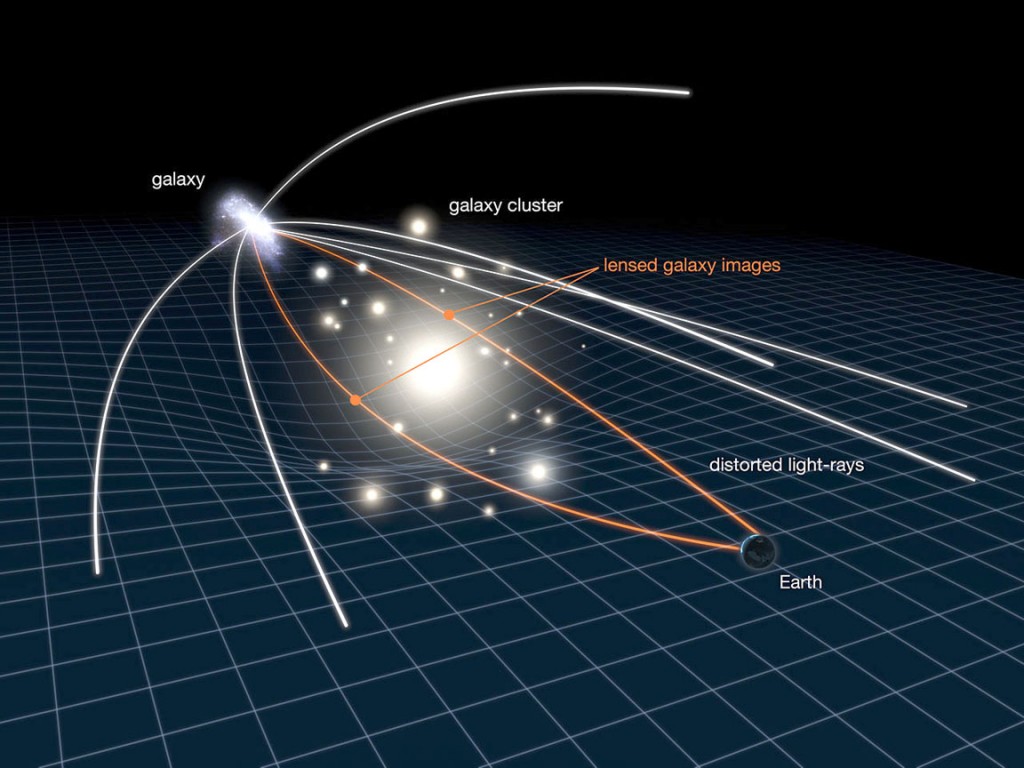Sungenis is more interested in the rhetorical capital he can make from Rosser’s statements than he is in adopting a self-consistent case for geocentrism. He would have his readers focus on the notion that the “[speed of] light can assume any numerical value” (in other words, in his rhetoric, any value that he needs it to have – his questioner on the Facebook page did indeed succumb to this interpretation), and gloss over the proviso “depending on the strength of the gravitational field”. Sungenis hides or is ignorant of the fact that the gravitational field is weak in a photon’s path from a distant star to the Earth. In the vast reaches of intergalactic space it is very, very much weaker than the gravitational field of the Sun at the Earth. It is somewhat stronger near massive galaxy clusters but only enough to create small perturbations in the photon’s path. It doesn’t affect the propagation of the photon to anywhere near the extent that Sungenis suggests. How do we know this? We know because we can observe the effect of gravitational fields on the light from stars and on the CMB, which causes the light from a single distant event to be deflected and so to appear at slightly different times in slightly different locations (an effect known as gravitational lensing) and to be red- or blue-shifted as it falls into or climbs out of gravitational wells near to large masses such as galaxy clusters (an effect known as the Integrated Sachs-Wolfe effect). Astrophysicists can quantify the size of these effects and deduce the magnitude of the gravitational field along the path of the photon from the star to the Earth – these fields are strong enough to change the arrival time of light from a distant supernova which is nine billion light years away by a few tens of years, but not to change it from 9 billion years to 6,000 years.[11]

And how about Sungenis’s fundamental idea that light consists of mechanical transverse waves in his aether, with the speed of light determined by the spring-in-tension expression for wave speed, v = √(T/μ)? This idea is an unnecessary non-starter because we have known since 1865 that light is an electromagnetic phenomenon and that the speed of light in a vacuum can be derived simply from two electromagnetic constants that were accurately measured in the 1850s. The two constants in question are the permittivity (ε₀) and permeability (μ₀) of free space[12]. In 1865 James Clerk Maxwell published his seminal paper on electromagnetism On Physical Lines of Force, in which he combined the laws of electricity and magnetism into a single unified theory and laid out the equations which describe electromagnetism. His fundamental formulation is the basis for all physics that involves electrical or magnetic phenomena, including the propagation of light. The speed of light was derived directly from the two constants referred to above which appear in Maxwell’s equations and which had previously been measured: c = 1/√(ε₀μ_0).

This equation for the speed of light based on the measured electromagnetic constants gives a value equal to the directly measured speed of light, and confirmed the hypothesis that light is an electromagnetic phenomenon. In addition to independent measurements of the two constants, an experiment to measure the ratio 1/√(ε₀μ₀₎ directly in an electromagnetic laboratory experiment in 1855 [13] yielded a value for c very close to the measured speed of light.

So, Sungenis’s naïve attempt to create an aether-based mechanical model for the propagation of light not only fails to predict what he wants it to predict, but it is anachronistic, wrong-headed and doomed to failure. It could only have been proposed by someone for whom the physics of electromagnetism and Maxwell’s equations is a deep and abiding mystery.

6 Conclusion

We have seen that Sungenis’s Planck-aether medium of geocentrism is an undetectable fantasy that exists only in his imagination. He plucks various propositions about its properties out of thin air and asserts them with bold but utterly misplaced confidence.

He states that light is a transverse wave in his invented medium and that its speed is determined by the tension between the hypothetical particles that make up the medium. He offers the analogy of a rotating spring to explain how the tension in the spring will result in the wave speed being greater away from the centre of rotation, and, by analogy, how the tension in the rotating aether will result in the speed of light being greater away from the Earth. We have seen that he gets the physics exactly backwards, and that the tension and thus the wave speed would be greatest at the centre, which would make the speed of light, according to his own idea, greatest at the Earth and less the further away you go.

Even in the case of a better analogy for Sungenis’s solid Planck-aether, a solid rotating disc, we have seen how the speed of transverse waves is greatest in the centre and less the further from the centre you go.

So Sungenis’s own model of light propagation gives results exactly opposite to what he asserts and what he wants them to be. And this discussion of rotating springs and discs, although entertaining and educational (particularly for Sungenis himself), is moot because light is not a transverse mechanical wave in a fantasy medium, but an electromagnetic phenomenon. The wave nature of light falls naturally out of Maxwell’s well-validated electromagnetic theory and the speed of light is related to two fundamental physical constants of electricity and magnetism measured in the 1800s.

In this and other articles (see here, here, here, and here), I have documented numerous examples of Sungenis’s profound ignorance of quite elementary physics and mathematics. Is any more needed to demonstrate that his physics is bad, his mathematics worse, and his expertise entirely inadequate to the task he has set himself?

 

End Notes:

[1] Galileo Was Wrong, Vol 1, Distant Events: Are They Past or Present?, p.262.

[2] ibid., page 263, reference 462

[3] When I was a post-grad, as a diversion, we made a film in the style of Monty Python. One sketch contained a satirical ditty about the discredited luminiferous aether. Who could foresee that in 2015 someone would actually believe in it? Sing it lustily to the tune of “God Save the Queen”:

In intergalactic space
The aether carries waves of star-origin
dah dah dah dah,

It sends them twinkling, propagated sparkling,

There must be something in empty space.

[4] A Planck particle, an entirely theoretical entity, is a hypothesised black hole, which has a Schwarzschild radius equal to its Compton wavelength. The Planck particle mass would be approximately the Planck mass (3.85 x 10^-8 kg) and its Schwarzschild radius would be approximately the Planck length, (5.73 x 10^-35 m). They are not thought actually to exist.

[5] The magnitude of the centrifugal force of a body revolving around an axis is given by:

where F is the centrifugal force, m the mass of the body, ω the angular speed and r the distance of the body from the axis. For the hypothesis of the rotating aether, the centrifugal force of a body at distance R from the Earth and at angle δ above the equatorial plane, the magnitude of the centrifugal force is:

So, for a given distance from the Earth, the centrifugal force would be maximum on the equatorial plane and would fall as cos δ, going to zero on the polar axis where δ = ±90°.

[6] Sungenis asserts that his aether doesn’t “react with baryonic matter” but with “electromagnetic and gravitational activity”. Interestingly, he asserts elsewhere that the aether “absorbs” the tremendous centrifugal force of stars rotating daily at astronomical distances (Answer to Camille Carlisle, p.3). He didn’t explain the mechanism there but now it seems that he thinks the aether doesn’t affect baryonic matter, the constituent of stars. The contradiction between these two evidence-free assertions seems to elude him. As does the contradiction within the very sentence quoted here, that the aether doesn’t “interact with baryonic matter” while “reacting” with “electromagnetic and gravitational activity”.

[7] Sungenis makes a distinct claim that if the spring is stretched to three times its length then the wave will travel proportionately faster due to the increased tension in the spring. In fact, the wave speed depends both on the tension and on the mass per unit length (the linear density) of the spring. Which one of these parameters dominates the wave speed depends on the stiffness of the spring, i.e. how much it extends for a given force. For a very stiff spring, one that requires a large force to achieve even a small extension (like a guitar string for example – the physics of transverse waves in tensioned springs and strings is identical), then the wave speed will depend mainly on the tension. Its length and thus its mass per unit length changes only very slightly. However for a spring with very low stiffness which is easily stretched with little force, like a slinky, the change in mass per unit length dominates. If we stretch a slinky by a factor of three, its mass per unit length also falls by a factor of three and this dominates the wave speed as the change in tension is minimal. So whether it’s the increase in tension or the reduction in mass per unit length that dominates depends on the stiffness. How does this affect Sungenis’s aether? Well, we don’t and we can’t know, and neither can he, because no-one can have any rational idea about a medium that is a pure fantasy and that has never been and cannot be detected in any way. We don’t and can’t know what its stiffness is and so we can’t say what effect stretching it will have.

[8] At any point r along the hanging spring, T is given by the weight of the spring itself below the point.

for a stiff spring, where T is tension, R is the length of the spring, g is the acceleration due to gravity on Earth and μ is the mass per unit length. For a stiff spring v ∝ √T, but for a spring which extends significantly under its own weight the wave speed depends both on T and on μ, but in all cases the speed is greatest at the top.

[9] At any point r along the whirling spring the tension is the integral of the centrifugal force acting on each element beyond the point:

 

where T is tension, R is the length of the spring, μ is the mass per unit length and ω is the angular speed of the rotation. So the tension falls as the square of the radius from the centre. It is maximum at the centre where r = 0 and falls to zero at the end where r = R.

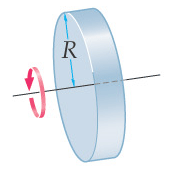
[10] For a solid rotating disc the stresses at a point r from the centre are given by:

 

 

where σ_r and σ_H are radial and hoop stresses respectively, R is the radius of the disc, ρ its bulk density and ν the Poisson ratio of the material. The maximum stress occurs in the centre, where the radial and hoop stresses are equal:

 

The maximum strain also occurs in the centre, according to Hooke’s law, and thus the density is lowest in the centre.

[11] See, for example, Kelly et al, Multiple Images of a Highly Magnified Supernova Formed by an Early-Type Cluster Galaxy Lens, http://arxiv.org/abs/1411.6009

[12] The permittivity of free space, ε₀, is a constant in Coulomb’s law which governs the force between two separated electrical charges. The permeability of free space, μ₀, is a constant in Ampère’s force law which governs the force per unit length between two parallel conductors carrying a current.

[13] This experiment was conducted by Wilhelm Weber and Rudolf Kohlrausch in 1855. See Joseph Keithley, The Story of Electrical and Magnetic Measurements, ISBN 0-7803-1193-0, p.115 et seq