[The thanks we receive for the material on Geocentrism Debunked is always encouraging. This reader’s comments were particularly thoughtful.]
———————————————————————————————————
Dear Mr. Palm,
I want to thank you for taking the trouble to run a website refuting geocentrism – I especially appreciate that you tackle the issues and show how Sungenis is wrong with polite, well-reasoned arguments. If you had simply mocked it and laughed it off as ridiculous I would not have listened to what you had to say. Instead, you refute Sungenis and other modern geocentrists using their own premises.
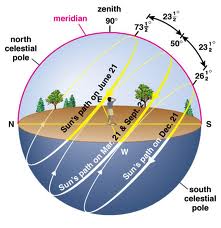 I encountered Sungenis’ geocentrism a few years back and was intrigued, but disbelieved it because I could not understand how he accounted for the seasons if the sun orbits the earth. I worked out on my own that it would have to sort of spiral from the Tropic of Capricorn to the Tropic of Cancer and back each year and that the center-point of that orbit would also have to move north and south, which didn’t seem likely. Last year a friend of mine revived my interest and I found that Sungenis does treat the sun (and the whole universe) as spiraling up and down, so that part “worked” – except that he never explained why the universe should oscillate in such a fashion. The stuff on the CMB and the “axis of evil”, and on the Michelson-Morley experiments, was also very intriguing, and it looked like there was proof that geocentrism would work and that the earth was motionless.
I encountered Sungenis’ geocentrism a few years back and was intrigued, but disbelieved it because I could not understand how he accounted for the seasons if the sun orbits the earth. I worked out on my own that it would have to sort of spiral from the Tropic of Capricorn to the Tropic of Cancer and back each year and that the center-point of that orbit would also have to move north and south, which didn’t seem likely. Last year a friend of mine revived my interest and I found that Sungenis does treat the sun (and the whole universe) as spiraling up and down, so that part “worked” – except that he never explained why the universe should oscillate in such a fashion. The stuff on the CMB and the “axis of evil”, and on the Michelson-Morley experiments, was also very intriguing, and it looked like there was proof that geocentrism would work and that the earth was motionless.
Your website has shown me that I was taken in by specious arguments, because I don’t understand many of the equations and principles of motion involved. I have a Ph.D. but not in any of the sciences, so like most people I’m not in a position to really evaluate an argument involving complex equations. Most people just follow the common opinion in such matters, but I have always been willing to entertain new, strange ideas. Geocentrism was such an idea. But the same willingness to challenge my own beliefs led me to take a look at your rebuttal. I suppose this is really a growth opportunity for me – instead of believing in heliocentrism only because that’s what I was taught in school, I can now believe it because I have some understanding of why it replaced the Ptolemaic view.
I think one of your articles pointed out that in the Ptolemaic system the earth really was believed to be the heaviest object in the universe [yes, see here]. I’ve read elsewhere of the old four-element system (earth, water, air, fire), in which the sun, moon, and stars are above the earth because they are made of fire, or even some lighter, special celestial element. There was also the view that the planets and stars were embedded in crystal spheres, which would also explain why they didn’t fall to the earth. The motion was explained by saying that supernatural agents moved the planets and stars. This system made sense to people for a long time because it didn’t contradict ordinary everyday experience, in which heavy objects fall and fire (heat) rises, and in which rocks don’t move themselves or anything else, but conscious agents such as people do move things. The problem for the new geocentrists is that they don’t believe the stars are made of a special, ultra-light matter, nor that the stars and planets move in crystal spheres or tubes pushed by angels, so then they do have the problem of answering a child’s questions: why don’t the stars and sun and moon fall down? What keeps them up in the sky? Why do they rise and set?
 MacAndrew’s article on your website was particularly helpful to me because it asked a simple question: can the mass of the stars really offset the gravitational pull of the sun so that the earth can be motionless and the sun in orbit? By putting in real numbers one can see that the answer is no [see Dr. MacAndrew’s “Here Comes the Sun”]. After that, it doesn’t matter what the Michelson-Morley experiments showed or didn’t show or what the CMB shows or any of the rest of it.
MacAndrew’s article on your website was particularly helpful to me because it asked a simple question: can the mass of the stars really offset the gravitational pull of the sun so that the earth can be motionless and the sun in orbit? By putting in real numbers one can see that the answer is no [see Dr. MacAndrew’s “Here Comes the Sun”]. After that, it doesn’t matter what the Michelson-Morley experiments showed or didn’t show or what the CMB shows or any of the rest of it.
You are right, too, to point out that the centrality of the earth was never important in Scripture or Tradition (I don’t think it’s even mentioned in Scripture). As for a motionless earth, Sungenis’ only real Scriptural argument (as you know) comes from Joshua’s miracle of “stopping the sun” (and the moon), but it’s really a quite weak argument, as you point out [see “Sungenis Binds What He Has Loosed on Joshua 10”]. The sun normally appears to move, and the miracle was that it didn’t, for about a day. Whether God actually stopped the sun or actually stopped the earth (and the moon) the experience for Joshua and his army was the same, and either way it was a miracle. I do believe in the inerrancy of Scripture, but not in the inerrancy of my own interpretation of it.
 Chesterton, in his book on St. Thomas Aquinas, has this to say about science versus Scripture: “If a literal interpretation is really and flatly contradicted by an obvious fact, why then we can only say that the literal interpretation must be a false interpretation. But the fact must really be an obvious fact. And unfortunately, nineteenth-century scientists were just as ready to jump to the conclusion that any guess about nature was an obvious fact, as were seventeenth-century sectarians to jump to the conclusion that any guess about Scripture was the obvious explanation. Thus, private theories about what the Bible ought to mean, and premature theories about what the world ought to mean, have met in loud and widely advertised controversy, especially in the Victorian time, and this clumsy collision of two very impatient forms of ignorance was known as the quarrel of Science and Religion.”
Chesterton, in his book on St. Thomas Aquinas, has this to say about science versus Scripture: “If a literal interpretation is really and flatly contradicted by an obvious fact, why then we can only say that the literal interpretation must be a false interpretation. But the fact must really be an obvious fact. And unfortunately, nineteenth-century scientists were just as ready to jump to the conclusion that any guess about nature was an obvious fact, as were seventeenth-century sectarians to jump to the conclusion that any guess about Scripture was the obvious explanation. Thus, private theories about what the Bible ought to mean, and premature theories about what the world ought to mean, have met in loud and widely advertised controversy, especially in the Victorian time, and this clumsy collision of two very impatient forms of ignorance was known as the quarrel of Science and Religion.”
Thanks again.



