Plagiarism: The Folly of Defending the Indefensible

by Dr. Alec MacAndrew (10 Oct 2014)

The geocentrists have been caught extensively plagiarising others’ work (see my article here and David Palm’s here). What is plagiarising? – it’s stealing the work of others and lying by pretending that it’s one’s own work. That they have done so, on several occasions, is incontrovertible – the evidence is overwhelming. Rather than admit to and apologise for this blatant ethical and moral failing, Bob Sungenis has attempted to brazen it out – see here. David Palm has done an excellent job of pointing out the absurdity of Sungenis’s position here, but I make a few points of my own below.

Sungenis has misrepresented me by repeating a certain statement in several different articles including this one. He boasts that I have “admitted” that General Relativity (GR) “permits geocentrism as a viable scientific theory.” This is a canard. I have not in the past, and I do not now “admit” any such thing. In fact, I have been careful to say from the very first time that I ever commented on geocentrism, and I have been utterly consistent since then, that geocentrism’s basic claims, that the Earth is absolutely static at the exact centre of the Universe, are meaningless according to GR. The statement that any object is absolutely static and at the exact centre of the Universe is meaningless within GR because GR does not address and answer such questions; within the framework of GR there is no absolute frame of reference and therefore there is no absolute rest or centre, the very things the geocentrists insist upon.  As to whether geocentrism is a “viable scientific theory,” as Sungenis puts it, this implies that he and his fellow geocentrists have actually made a scientific case — something they are yet even to begin.

Sungenis attempts to defend the plagiarising of 23 pages of others’ work:

…the same equations heliocentrists use to demonstrate the viability of their system can be used to demonstrate the viability of the geocentric system, which has been known ever since Mach and Einstein expanded on Newton’s equations. The geocentric derivations MUST employ the heliocentric equations, often point-for-point, since the geocentric is just the inverse of the heliocentric. There is no way to avoid this state of affairs, especially when one is trying to show the equivalence of the two systems. MacAndrew simply doesn’t like the fact that it is so easy to derive the geocentric equations from the heliocentric (“David Palm Falsely Accuses Opponents of Plagiarism”, p. 4f.).

According to this nonsensical defence, if Bouw and Sungenis wanted to respond to the challenge of deriving the Lagrange points in a geocentric framework by simply claiming that the equations are identical to the standard derivations, then why didn’t they just say so and refer the reader to the Moulton textbook and the Cornish tutorial? Why did Bouw produce 23 pages of directly plagiarised content while pretending to be doing his own derivation within the geocentric framework?

He did this, of course, because the simple claim that the maths is identical in the geocentric and conventional frameworks, a claim that Sungenis has now been forced to make in order to defend the indefensible, is deeply unconvincing, and so Bouw felt he had to lie and cheat about what he was doing. By plagiarising Moulton’s textbook Bouw is engaged in cargo cult physics. (I need hardly add that Sungenis’s trumped up “defense” that Moulton’s work is out of copyright is foolish – the fact of plagiarism does not depend on whether the plagiarised work is in or out of copyright; if one copies others’ work and presents it as one’s own, then one is a plagiarist).

Moreover, claiming that the text book results are the same in a geocentric framework, is not only unconvincing, but it’s wrong. Both derivations, that of Moulton in the 1914 textbook and that of Cornish in the modern tutorial, are based entirely on Newtonian physics. The Lagrange points are points where the gradient of the effective potential of the three body system is zero – the effective potential is defined as the sum of the gravitational potential arising from the masses of the bodies plus the potential energy arising from the centrifugal effect of their rotation. In others words, it is inherent and essential in the textbook solutions plagiarised by Bouw that the Sun and Earth are orbiting their centre of mass – the Moulton and Cornish derivations (and indeed all other solutions to the restricted three-body problem) explicitly exclude a static Earth. So, Bouw has lost his reputation for honesty in order to present a solution that doesn’t actually support his case. That is pathetic.

Finally, I note that Sungenis equivocates:

Moreover, MacAndrew’s charge that Bouw’s paper contains “errors in math” was already answered. They aren’t errors. They are disagreements MacAndrew has regarding how to apply the math (ibid., p. 5).

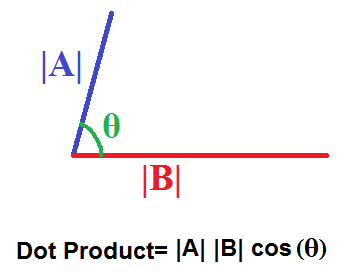Sungenis is obviously a mathematical ignoramus, to be presented so clearly with what is a mathematical error and to persist in attempting to excuse it. The charge I made is unanswerable because the error is obvious, simple and incontrovertible. In maths, there is a right and a wrong answer. Bouw has given the dot product of two orthogonal vectors as a non-zero quantity. But the dot product of two orthogonal vectors is identically zero, in all circumstances, and so Bouw has made a mathematical blunder which feeds through his derivation to the end rendering his conclusion wrong. This is not a matter of interpretation, or opinion, but a matter of fact. Anyone who has any grounding at all in linear algebra can see that that is the case. The more Sungenis cavils, the more absurd he appears.

Sungenis has a policy never to admit he is wrong and always to respond to critics no matter how egregiously wrong he is (and he is, often, egregiously, hopelessly wrong). This policy has the disadvantage that the more he attempts to defend the indefensible, the more ridiculous he appears. In his “defense” of Bouw’s and his own plagiarism, he looks very ridiculous indeed.