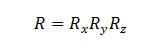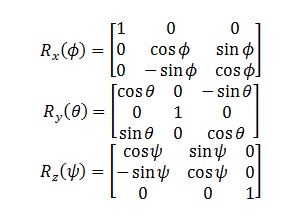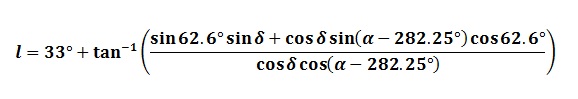by Dr. Alec MacAndrew
1 The high priest of geocentrism
Mr Robert Sungenis is woefully uneducated in science and mathematics. Despite this, he is widely acknowledged by the geocentric community as an expert in scientific matters, even by apparently intelligent people such as geocentrist Rick DeLano, who should, or at least could, know better. Sungenis writes “scientific” books, gives presentations and hosts a Facebook page where he invites people to ask him about science. For that tiny handful of true believers in geocentrism, those who are totally invested in it, he can do no wrong. For them, he is an authority on a par with the world’s best theoretical and experimental physicists.
In February of 2015 we issued the “CMB Alignment Challenge” to the geocentrists. The terms of that challenge were very clearly spelled out.
Mr Sungenis has now made two responses to this challenge – one in the comments box of a post on his Facebook page here, and a second more formal response on his website here. I will focus on the latter in analysing the grievous mathematical and physics mistakes that he makes, although I’ll touch on the former briefly.
Anyone who has been following these discussions on geocentrism will be aware of Sungenis’s mathematical incompetence. For example, he has still failed to correct the neo-geocentric derivation of forces in a rotating universe here on page 61, where he makes the scalar product of two orthogonal vectors non-zero, many months after I have explained to him in “There He Goes Again” the fact that the scalar product of orthogonal vectors is zero by definition of the scalar product.
His attempts to calculate what the centrifugal force would need to be if the Sun is rotating about the Earth provided us all with a great deal of hilarity in “Sungenis Botches the Math Again”: in his first article he used an expression that didn’t even have the right dimensions and was numerically wrong by a factor of a million. Even after I pointed out the right answer and actually did the calculation in excruciating detail for him, he still got it wrong on his second try by a factor of ten thousand million million million!
A third egregious example (out of many) can be found in footnote 5 of his piece here where he presents this sum that an eighth grader should get right. He writes: 1030 x 1035 – 186,000 = 1059. He is out by a factor of a million! (Needless to say, in addition to getting the sum wrong, the entire basis of his calculation is balderdash, but let’s focus here on his grossly bad arithmetic and leave his “physics” for another time.)
Why do I mention these past blunders? Because he blunders mathematically again and again in his fruitless attempt to answer the CMB Challenge. Added to his many past mistakes, this paints a vivid picture of hopeless mathematical ineptitude.
Before we get started on the detail, notice that Sungenis’s response to the challenge contains much geocentric rhetoric about the unexpected and anomalous alignment between the dipole, quadrupole, octopole, and the ecliptic plane and equinoxes. I remind readers that, in the original Challenge, we took pains to point out that we agree that these alignments are unexpected and currently unexplained – in fact, I discussed them in some detail here. However the challenge is not focused on that aspect of the question but on whether I calculated the alignments correctly. See the explicit terms of the Challenge here.
Readers will also remember our explanation here and my more technical demonstration here that the anomalies, such as they are, do not support the geocentric proposition. The geocentrists’ florid claims that the CMB multipoles point directly at the earth are based on a deep misunderstanding of the anisotropies in the CMB since the multipoles do not point at anything – they do not pick out any position in space, and furthermore they originate at the observer by definition.
Therefore, I shall leave discussion about the cosmological significance of the low multipole alignments for another article, and focus in this one on the calculations to quantify how close or approximate the alignments actually are – which is, after all, what the Challenge is about.
The sort of confused and error-strewn performance that we will see him engage in here provides ample evidence that Sungenis, replete with degree-mill “PhD”, proven plagiarist and mathematical incompetent, is a pseudoscientist and a scientific charlatan. I don’t make these judgements lightly, but no other conclusions are possible in the face of the multiple elementary bungles he makes here and elsewhere.
There is no shame in not knowing about a subject, but there should be shame in not knowing and yet pretending that you do, especially when you use your counterfeit knowledge to bamboozle others.
I’ll show in this article that Mr Sungenis has not only failed to answer the CMB Challenge that we set him (see here), but that in his attempt to do so here he makes many woeful mathematical and conceptual mistakes. The title of his reply, “The CMB Alignment Challenge – Answered, Put to Bed, and Counter-challenged”, reeks of unjustifiable hubris. He might hope that he has answered the Challenge and put it to bed, but actually, he fails abysmally.
Furthermore, it is implicit in his reply that I was right when I demonstrated that the alignments of the CMB features with themselves and the ecliptic and equinoxes are inexact.
The major errors made by Sungenis, which I will expand upon in the referenced sections of this article, are:
- He produced an earlier response to the challenge with entirely different but equally erroneous analyses (section 3).
- He defines the ecliptic as a single direction or vector, whereas it is a plane that cannot be defined by a single direction (section 4).
- The direction he assigns to the ecliptic does not even lie in the ecliptic plane (section 4).
- His suggested expression for calculating the angle between two directions depends on how the directions are labelled and is not co-ordinate system invariant (section 7).
- He inexplicably uses the wrong component separation algorithm (SEVEM instead of SMICA) to specify quadrupole and octopole directions, even though the original CMB Challenge was very clear that SMICA should be used (section 8).
- He claims that a probability of 0.009 is “about 1 in 10,000” when actually it is about 1 in 100, an error on his part of a factor of 100, yet another elementary arithmetical blunder (section 10).
- Based on the direction of the Axis of Evil quoted in Kate Land’s presentation, he makes a bogus estimate of the quadrupole to equinox angle (section 12).
- He does a nonsensical calculation to get the quadrupole to dipole angle, by simply subtracting angles between non-planar directions that lie in 3D space (section 12).
- He calculates (incorrectly) and presents (proudly) hugely discordant angles between the quadrupole and equinox, and between the quadrupole and dipole, without recognising the absurd degree of discrepancy (section 12).
- He calculates angles to the ecliptic plane incorrectly: he does so by calculating the angle to the erroneous vector he assigned to the ecliptic earlier on, and he clearly has no idea how to calculate the angle between a vector and a plane (section 13).
- He confuses longitude and latitude (section 15).
- He plots the angles between directions on a diagram that shows only the component of latitude of each direction (section 15).
The article that we will analyse here in detail is not the first attempt Sungenis has made to answer the CMB Challenge. In fact, a few weeks before he posted this article on his web-site, he posted a response to the challenge in the comments box of his Facebook page “Ask Robert Sungenis”. That response can be found in this Facebook page here, but since the entire response spanned several separate comments, I’ve gathered the whole screed together for ease of reading here.
The most interesting thing about his response on the Facebook page is that it embodies an entirely different species of wrongness from the abject display that we analyse here. I have no intention of going through his Facebook post in the same sort of detail in which I address his website article – that would be too tedious for me and for the reader. The fact is that they are both riddled with laughable errors.
The key point is that Sungenis has given, in public, entirely different and incompatible answers to the same questions. And he has done so without acknowledging or recognising it. Such a display would be inconceivable for a scientist. It is powerful evidence that Sungenis does not understand the foundations of the topics he attempts so incompetently to engage in, and that he doesn’t care about consistency or accuracy, but merely about an ersatz appearance of authority and knowledge.
It is indeed the case that Sungenis just makes it up as he goes along.
4 Sungenis starts badly, very badly
Turning to the more recently posted response, the first paragraph of Sungenis’s section entitled “Answer to Challenge” is:
MacAndrew and Palm have consistently sought to answer the CMB and galactic alignments by asserting that they are not precisely what we claim. They claim we have exaggerated the CMB and galactic alignments and have made it sound as if the alignments are directly on the same line with the Sun-Earth ecliptic (RA = 180°, δ = 23.5°) and the Earth’s autumnal equinox (RA = 180°, δ = 0°).
In just the second sentence of his reply he makes two appalling mistakes about the ecliptic, based on his fundamental ignorance of elementary geometry and his misunderstanding of what the ecliptic plane is, and how it is described in equatorial co-ordinates. What’s more, he will repeat these mistakes later in some of his calculations, rendering them plain wrong.
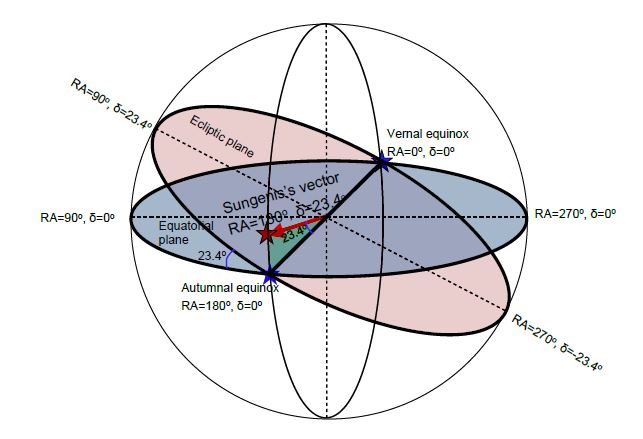
His first mistake is to treat the ecliptic as a direction. But the ecliptic is a plane and so cannot be defined by a single direction. A plane can be defined in a number of ways (e.g. by specifying three non-collinear points, or by two intersecting or parallel lines, or by a line and a point that doesn’t lie on the line) but never by a single line. The ecliptic is not a direction, but the plane in which the Earth orbits the Sun and it intersects the equatorial plane (the plane in which Earth’s equator lies) at an angle known as the obliquity of the ecliptic, ε, which is about 23.4° (in other words the Earth’s equator is tilted by about 23.4° to the plane of the ecliptic). (Note: Sungenis quotes ε as 23.5° and I quote it as 23.4°; the difference is insignificant, and due to rounding and choice of epoch: it is actually 23.4393° in J2000.0 – see the 2010 Astronomical Almanac)
Since Sungenis works in equatorial co-ordinates throughout his reply, let’s look at how the ecliptic plane should be specified in that system (we’ll encounter two other celestial co-ordinate systems later in this article). The primary direction of the equatorial co-ordinate system is towards the vernal equinox which is defined as RA=0°, δ=0°. (Note that, strictly speaking, the longitude in equatorial co-ordinates is designated RA and measured in hours:minutes:seconds; or α, and measured in decimal degrees – for the sake of simplicity we use RA and α without distinction and report the longitude in decimal degrees.) The equinoxes are points on the celestial sphere intersected by the axis formed by the intersection of the ecliptic and equatorial planes, their nodal line, so, by definition, the direction RA=0°, δ=0°, the ascending node of the ecliptic, lies on the ecliptic plane and on the equatorial plane. That single direction is insufficient on its own to fully define the ecliptic plane, for which we need a second direction, for example RA=90°, δ=23.4°. Specifying these two directions, RA=0°, δ=0° and RA=90°, δ=23.4°, uniquely defines the ecliptic plane, and I must stress that two directions are needed to define the plane.
Figure 1 showing the relationship of ecliptic and equatorial planes and the equinoxes. The equatorial plane is blue, the ecliptic plane is pink and the directions of the equinoxes are towards the blue stars lying on the intersection of the two planes. The single direction that Sungenis quotes for the ecliptic is the red star that doesn’t even lie in the ecliptic plane
If you consider the co-ordinates for the second direction I used to define the ecliptic, RA=90°, δ=23.4°, you will see that a direction, lying in the ecliptic plane, which has a declination equal to the obliquity of the ecliptic, ε = 23.4°, occurs at a right ascension of 90° not at 180° as Sungenis would have it (and a declination –ε occurs at right ascension 270°). (Another way of looking at this is that the sun is directly overhead at midday on the equator at the vernal and autumnal equinoxes, RA=0° and 180°; it lies 23.4° north at midday on the equator at the summer solstice, RA=90°; and at 23.4° south at the winter solstice, RA=270°.)
So Sungenis’s specification of the ecliptic is wrong, not just because he treats it as a direction rather than a plane, but also because the direction he specifies doesn’t even lie in the ecliptic plane. His “ecliptic” direction, RA = 180°, δ = 23.5°, has nothing to do with the ecliptic plane. It is doubly wrong. See Fig 1.
Sungenis’s elementary misunderstanding of the ecliptic is bound to have serious consequences when he comes to calculate the angle between various CMB vectors and the ecliptic, which we shall come to later, but these errors in themselves highlight his ignorance of geometry and the specification of directions in various celestial co-ordinate systems. He is simply not fit to do these calculations, to engage in scientific debate or to attempt to school others.
I mentioned earlier that there are three celestial co-ordinate systems that I use in this article. So what are they, and how are they defined? Celestial co-ordinate systems are used by astronomers and cosmologists to specify the direction to astronomical bodies and features. They are generally spherical co-ordinate systems, which have a defined origin and in which the direction is specified by a longitude which runs from 0° to 360° or 0° to ±180° or 0 to 24 hours and by a latitude which runs from +90° to -90°. The longitude is measured in the fundamental plane of the co-ordinate system starting with 0° towards the primary direction, a direction chosen by convention which lies in the fundamental plane. The latitude determines the angle above or below the fundamental plane. Taken together, the origin, the fundamental plane and the primary direction, along with a sign convention, uniquely define a co-ordinate system. Let’s summarise the three co-ordinate systems used by astronomers that are relevant to this article:
- The equatorial co-ordinate system: its fundamental plane is the plane of Earth’s equator and the primary direction is towards the vernal equinox. Longitude is called right ascension, RA or α. Latitude is called declination or δ. Astronomers usually measure right ascension in hours:minutes:seconds, but it can also be measured in degrees as both Sungenis and I do here.
- The ecliptic co-ordinate system: its fundamental plane is the ecliptic plane, and the primary direction is again towards the vernal equinox. The ecliptic longitude is usually notated as λ and the latitude as β.
- The galactic co-ordinate system: its fundamental plane is the plane of the Milky Way galaxy and its primary direction is towards the galactic centre. Galactic longitude is notated as l and galactic latitude as b
Since there are these three (and other) different celestial co-ordinate systems, when giving the co-ordinates of a direction in astronomy, it is essential to specify which co-ordinate system is being used.
6 The basis for co-ordinate transformations
How do we express the co-ordinates of a feature in, say, ecliptic co-ordinates, if we have them in, for example, galactic co-ordinates? To do this, we need to carry out what is called a co-ordinate transformation. If you recall, part of the CMB Challenge was for the geocentrists to show how they did this:
- Do the calculations to transform the direction of the dipole, quadrupole, octopole and equinox, as required, to galactic or ecliptic co-ordinates so as to be able to calculate the angles between them…
- Publish your work on-line, including, on-line, your working for calculating both the coordinate transformation and the angles.
Sungenis ignored this part of the challenge. Since the co-ordinate transformations that he quotes are correct, for the most part, it is likely that he used one of the several available on-line astronomical co-ordinate transformation tools (see here and here). So although he failed this part of the challenge, I’m inclined to let it pass, since his omission pales into insignificance alongside the enormous howlers that he made. His sins of omission are less serious than his sins of commission. For completeness, I have attached an appendix which explains the mathematical basis of the astronomical co-ordinate transformations.
7 The basis of the angular calculation
Given the direction of various features of the CMB and the equinox in any one celestial co-ordinate system, one can calculate the angle between any of these vectors. The CMB Challenge included these requirements:
- Calculate the eight angles between these vectors, the equinox and the ecliptic plane as presented in “The CMB and Geocentrism” and reproduced above.
- Publish your work on-line, including, on-line, your working for calculating both the co-ordinate transformation and the angles.
The co-ordinates of any one feature, say the SMICA KQ corrected quadrupole, are different depending on which co-ordinate system one chooses to express them in. The relevant Planck paper gives the quadrupole direction in galactic co-ordinates, and according to that paper, the KQ corrected SMICA quadrupole is at l=224.2°, b=69.2°. In ecliptic co-ordinates the same feature is at λ=163.1°, β=16.0°. And in equatorial co-ordinates, it’s at α=170.9°, δ=21.4°.
Therefore, the co-ordinates of any feature are not invariant under co-ordinate transformations. However, the angle between any two features is invariant. It doesn’t matter in which co-ordinate system you do the sums, the angle between two lines or two vectors or two directions should result in the same numerical value. So, any expression you use to determine the angle should not depend on choice of co-ordinate system. You should get the same result for the angle between directions whether you work in any of the spherical co-ordinate systems that we have mentioned (galactic, ecliptic or equatorial) or in any other arbitrary spherical co-ordinate (or, indeed, in Cartesian co-ordinates or other co-ordinate systems).
With that in mind, let’s look at Sungenis’s suggested expression for calculating the angle between two directions in celestial co-ordinates:
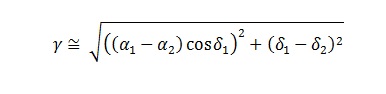 where γ is the angle between them, α1 and α2 are the longitudes, and δ1 and δ2 are the latitudes of the two directions.
where γ is the angle between them, α1 and α2 are the longitudes, and δ1 and δ2 are the latitudes of the two directions.
We can see immediately that the first term of his expression depends on δ1 but not on δ2. However, the choice of which direction is labelled 1 and which is labelled 2 is arbitrary. Sungenis’s expression gives a different answer depending on which direction you label 1 and which you label 2 (except in the trivial case where the declinations of the directions are the same), whereas it should yield the same angle independent of how you label the directions. It gives very poor results at higher latitudes or with bigger angles and seems to be a misquotation of the equirectangular approximation:
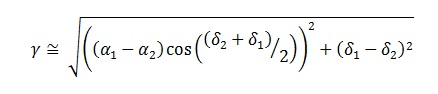 This approximation, which at least yields results independent of how the directions are labelled, gives reasonable results for cases where the directions lie at small latitudes and where the angle between them is small. It becomes increasingly inaccurate with increasing latitude or where the angle is larger. For example, it gives poor results in galactic co-ordinates for the directions we are concerned with here. It is an approximation because it depends on plane geometry whereas the exact expression should be calculated using spherical geometry, as it is based on spherical triangles in which the angles do not sum to 180°. Since the expression that is exact for all angular separations and at all latitudes and in all co-ordinate systems is hardly more complicated, then why not use it? There is no need for an approximation.
This approximation, which at least yields results independent of how the directions are labelled, gives reasonable results for cases where the directions lie at small latitudes and where the angle between them is small. It becomes increasingly inaccurate with increasing latitude or where the angle is larger. For example, it gives poor results in galactic co-ordinates for the directions we are concerned with here. It is an approximation because it depends on plane geometry whereas the exact expression should be calculated using spherical geometry, as it is based on spherical triangles in which the angles do not sum to 180°. Since the expression that is exact for all angular separations and at all latitudes and in all co-ordinate systems is hardly more complicated, then why not use it? There is no need for an approximation.
So what is the exact expression? The angle between two directions (α1, δ1) and (α2, δ2) in any given spherical co-ordinate system is the central angle subtended by the great circle arc joining the points where the two directions intersect a sphere. The central angle is derived from the spherical law of cosines, and this expression is exact in all co-ordinate systems:
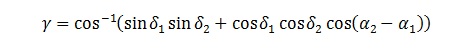 One can also use the (also exact) haversine expression which is computationally better conditioned for small angles.
One can also use the (also exact) haversine expression which is computationally better conditioned for small angles.
For example, if we use Sungenis’s expression to calculate the angle between the SMICA kinematic corrected quadrupole reported by the Planck team and the equinox in galactic co-ordinates (quadrupole (l, b) is at (224°.2, 69.2°), equinox (l, b) is at (276.337°, 60.188°), then the angle between these directions given by Sungenis’s expression is 20.59° if one labels the quadrupole as 1, and 27.44° if one labels the equinox as 1. The correct angle, given by the exact expression quoted above is 23.15°
8 Choice of component separation algorithm and other Sungenis errors
A component separation algorithm is applied to the raw data returned from the CMB missions in order to separate contributions to the CMB map from various astrophysical sources such as dust, free-free and synchrotron emission, and to separate distortions in the anisotropies caused by effects such as the late Sachs-Wolfe effect and the Sunyaev- Zel’dovich effect from the primordial anisotropies. In fact the Planck team applied and published data based on four different component separation algorithms (Commander-Ruler, NILC, SEVEM and SMICA).
Since each component separation algorithm gives slightly different results for the directions of various CMB features, I was very careful to specify which I had used in my calculations, and the use of results from the same algorithm was explicitly required by the terms of the challenge:
The vectors for the quadrupole and octopole in galactic co-ordinates are to be taken from the Planck paper, Planck 2013 Results. XXIII. Isotropy and statistics of the CMB, Table 18, p21, the final row (SMICA component separation algorithm, kinematic quadrupole corrected)
However, Sungenis uses data derived from the SEVEM component separation algorithm in those of his calculations that include the quadrupole and octopole, which, along with his inaccurate expression for the angle, explains why he gets a somewhat different answer from me for the quadrupole-to-equinox and octopole-to-equinox angles. Having obtained a different result by using data based on a different component separation algorithm from the one I used and specified, he claimed that he was “correcting” my calculations. His use of Planck data different from that specified can be explained only by carelessness or deliberate dishonesty.
The fact that my calculation was correct can be easily checked by putting the KQ corrected SMICA data for the quadrupole (l=224.2°, b=69.2°) and octopole (l=239.0°, b=64.3°) from Planck 2013 results, and the direction of the autumnal equinox in galactic co-ordinates (l=276.34°, b=60.19° transformed from λ=180°, β=0° in ecliptic co-ordinates) into the exact expression for the angle that I quoted above. Alternatively you could transform the quadrupole and octopole directions to ecliptic or equatorial co-ordinates and use (180°, 0°) as the direction for the autumnal equinox. In either case you’ll get the same result that I originally quoted in the CMB challenge. I carried out the calculations correctly in every case.
9 Sungenis floats yet another conspiracy
On page 8 of his paper, Sungenis makes a remarkable claim:
…it is important to know that although the measurements for the CMB alignments have not changed much between WMAP 3 and the first year Planck analysis (a span of about 10 years), the angular distance between the quadrupole and octopole has suffered the greatest change. It has increased by 1400% from its original .5° to its present 7.69°. Prior to 7.69°, there was a half-step to 3°, as noted in the below article. The point to be made here is, the larger they can make the separation, the better it appears for the Copernicans and MacAndrew…
This is tantamount to claiming that the poorer alignment between quadrupole and octopole as measured by the more precise Planck mission versus the earlier less precise WMAP mission is the result of a conspiracy amongst scientists to minimise the significance of the data. No scientist would make such a claim. But of course, Sungenis, even when he is trying to present a sober scientific case can’t resist succumbing to conspiracy theories (this is hardly an isolated case: see “Piling On, or Holding Back?“).
10 Getting the probabilities wrong
He then goes on to claim:
…even though 7.69° doesn’t even come close to solving their problem, since the “Probability” column in Table 18 for even a high figure like 7.69° is “0.009,” or about 1 in 10,000
This demonstrates his arithmetical incompetence, since a probability of 0.009 is about 1 in 100 (1 in 111 to be more precise), not 1 in 10,000. So Sungenis yet again gets a calculation wrong by more than one order of magnitude.
11 Confusing the WMAP and Planck data
His carelessness continues as he attributes a long quote on page 9 of his article to the Planck experiment when in fact it is from the final year (Year 9) WMAP summary paper (Bennett, C.L., et.al., Nine-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Final Maps and Results, ApJS., 208, 20B, available here)
Interestingly too, he curtails the quote from the WMAP team before the end. It reads:
We conclude that our ability to remove foregrounds is the limiting factor in the measurement of the cosmological quadrupole-octupole alignment. The already low statistical significance (<3σ) of the estimated alignment must be further degraded by the posterior selection made to examine this particular quantity. Given that there is no evidence of experimental systematic effects, and that the foreground-CMB separation contributes substantially to the alignment uncertainty, the estimated alignment appears to be a low-significance chance occurrence. (Emphasis added).
12 Bungling other data sources
The CMB Challenge was very straightforward – to do the calculations for the angles between the various features based on clearly specified data from the Planck mission and to show his workings. But Sungenis failed to do this. The fact that he drags in data from a many other sources is an obvious attempt to obfuscate his failure.
Not content with choosing data from the incorrect Planck component separation algorithm, Sungenis introduces other calculations and commentary based on an entirely different and earlier CMB mission, WMAP. These include some discussion from a seminar presentation by Kate Land about the alignments here (who, at the time, was Joao Magueijo’s PhD student and post-doc – coincidentally in the same department where I did the research for my PhD and where I was a post-doc many years before), and from a presentation by Michael Longo presenting his study of asymmetry in spiral galaxy handedness and its alignment with the CMB features as a foundation for his speculative explanation for the alignments.
Land’s presentation follows the outline of the well-known Land and Magueijo paper on the alignments and is based on first year WMAP data. Land and Magueijo found a direction in the alignments at (‑100°, 60°) in galactic co-ordinates (note that this is the same as (260°,60°)) which was the mean direction of multipoles l=2 to 5, and which they dubbed, tongue in cheek, the Axis of Evil (AoE); Tegmark et al did a similar analysis in this paper. Sungenis takes the AoE datum and calculates the angle between the AoE and the equinox and dipole correctly (he uses a very slightly different datum for the dipole from the one I specified, but it is close enough). He then says (page 11):
If we double Land’s figure for the Axis of Evil to the equinox (since the Axis of Evil is orthogonal to them) in order to get the approximate angular separation between the quadrupole to the equinox, the
quadrupole to equinox is 16.26°, which would leave the
quadrupole to dipole at about 2.04°
This is grammatical and computational drivel. First, it is impossible to parse the statement “since the Axis of Evil is orthogonal to them”, because there is no possible referent for “them”. The AoE is, in fact, not orthogonal to any of the directions under discussion, so heaven only knows what Sungenis means. Second, it is quite impossible to estimate the quadrupole-equinox angle by doubling the AoE-equinox angle – there is simply no mathematical or physics justification for doing that.
Next, having generated an entirely spurious quadrupole-equinox angle using a nonsensical calculation, he then engages in even more buffoonery by subtracting the dipole-equinox angle from the spurious quadrupole-equinox angle to get a bogus quadrupole-dipole angle. You can’t just subtract angles in three dimensional space as he does here – that shows a fundamental lack of understanding of the spherical trigonometry and the layout of the directions in 3D space. And Sungenis’s bungled attempts to estimate these angles are pointless anyway because the directions of the quadrupole and octopole are given clearly in the Planck paper, and this allows the direct computation of the quadrupole/octopole to equinox and quadrupole/octopole to dipole angles using the exact expression I referred to above, and these angles are as I quoted them in the original CMB challenge. This is another serious failure for Sungenis.
Sungenis quotes the direction of the quadrupole based on WMAP data in Longo’s presentation here and refers to it as the “corrected” quadrupole direction. The claim that the WMAP data he uses represents a “corrected” data point is preposterous, since the Planck data that we specified in the challenge is the most recent source of data and more precise than earlier WMAP data. Using the WMAP data, Sungenis calculates the quadrupole-equinox angle as 21.06° (23.1°) and quadrupole-dipole as 26.70° (28.5°) (the angles in brackets are the ones I provided using the Planck data and they are correct, based on the specified dataset).
The choice of data was precisely defined in the challenge, and so resorting to other sources of data can only be interpreted as Sungenis’s disingenuous attempt to avoid admitting that I was correct. Note also the large disparity between the quadrupole-equinox and quadrupole-dipole angles that he calculated himself, based on the Land presentation, compared with the same angles he calculated based on the data from the Longo presentation:
| Sungenis calculation based on Land presentation | Sungenis calculation based on Longo presentation | |
| Quadrupole to equinox | 16.26° | 21.06° |
| Quadrupole to dipole | 2.04° | 26.70° |
The quadrupole to dipole is especially discordant and it is interesting that Sungenis presents these totally incompatible results without the slightest sign of cognitive dissonance – does he even realise how absurd it is to make these incompatible claims? He clearly has no idea of what he’s talking about.
13 Misunderstanding the ecliptic
Remember the fact that Sungenis started badly, very badly? He not only defined the ecliptic as a direction, when it is in fact a plane, but the direction he quoted, (RA=180°, δ=23.5°), does not even lie in the ecliptic plane (see section 4 above).
Now the chickens are coming to roost: Sungenis uses this incorrect representation of the ecliptic to calculate angles from the dipole, quadrupole and octopole (using WMAP year 3 data as quoted by Longo) to the ecliptic plane. Of course the angles he gets (32.34°, 9.39° and 13.06° for the dipole, quadrupole and octopole respectively) are complete garbage as he is actually calculating the angle between the CMB features and a direction that has nothing whatever to do with the ecliptic. It will take the most dedicated, ill-informed and duped acolytes to take Sungenis seriously again after this inept display.
So, how does one calculate the angle between a line and a plane? The angle, let’s call it θ, can be calculated by noting that the angle between the line and a normal to the plane which intersects the plane at the same point as the line is 90°- θ. So we can use the normal to the ecliptic plane (β=90°) and calculate the angle between that and the CMB features in ecliptic co-ordinates and then take 90°- (that angle). But there is an even easier way if one transforms the dipole, quadrupole and octopole directions to ecliptic co-ordinates – the angle between the ecliptic plane and the CMB directions is simply the latitude, β, of each CMB feature in ecliptic co-ordinates, and this is so by definition, as the fundamental plane of the ecliptic co-ordinate system is the ecliptic plane, so the latitude of a direction gives the angle between the direction and the plane by definition.
Needless to say that the values I quote for the dipole, quadrupole and octopole to the ecliptic plane are correct, and Sungenis’s fumbling attempts are hopelessly, disastrously wrong.
On page 15 of his article, Sungenis presents a meaningless table into which he pours many of the appalling schoolboy blunders that we have seen him make. Let’s look at this table column by column.
In column 2 of the table he lists the angles I reported, which, as we have seen, are correct when starting with the specified SMICA KQ-corrected Planck data.
In column 3, he lists what he calls Longo data. The first point to make is that the data quoted by Longo is from WMAP Year 3 so we expect to find a modest difference between that and Planck 2013 data when considering the same angle (as ever Sungenis introduces other data sources to avoid agreeing that my calculations were correct). Second, Longo quotes two of the three octopole area vectors (also known as normal vectors, and defined in this paper), and they have a different mathematical basis from the single MAMD vector (Maximum Angular Momentum Dispersion defined in this paper) used by the Planck team to specify each of the multipole directions. I have explained in this technical article here the difference between the area and MAMD vectors. For the casual reader, all you need to know is that although area and MAMD vectors lie near to each other, they are mathematically different and cannot be directly compared. Those Sungenis errors apply to all the data in the Longo column, but the final three data which report angles to the ecliptic plane also include his disastrous bungle explained in Section 13 above, in which he completely mis-characterises the ecliptic plane.
Column 4 contains what he calls Land/Cruz data, but the two points involving the quadrupole are a reiteration of his nonsensical calculation from page 11 of his article which I covered in Section 12 above.
In column 5 he lists what he optimistically calls “corrections” to my calculations. The first three angles are moderately different from mine mainly because he uses data based on a different component separation algorithm, and the last three which are angles to the ecliptic plane are substantially and erroneously different because they are based on the same ecliptic plane bodge that we discussed above in Section 13.
In column 6, he takes the average of the data in the previous columns. Why one should want to do this remains mysterious, and Sungenis never refers to or uses the numbers reported in that column, possibly because even he realises that they have neither meaning nor use.
15 Confusing longitude and latitude
On page 17 of his article, Sungenis introduces a discussion in which he attempts to use the data to diagrammatically represent the directions of the various features. He bases his diagram on one included in Michael Longo’s seminar presentation here, which shows the right ascension components of various directions in a diagram looking down on the equatorial plane (in the plane of the paper) (Fig 2). Of course, as soon as one extracts components of two-dimensional directions into a one-dimensional diagram, one has to be careful to use only those components – in Longo’s case his diagram is based only on the right ascension components of the directions. (This shouldn’t be confused with the common representation of cosmological vectors where the directions are represented by points on the celestial sphere and the two-dimensional surface of the sphere is represented on a flat surface as a map projection.)
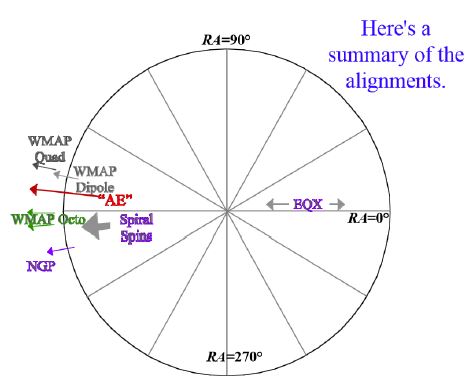 Fig 2: Longo’s diagram that shows the right ascension of various features. This diagram is constructed looking down at the equatorial plane (the blue plane of Fig 4)
Fig 2: Longo’s diagram that shows the right ascension of various features. This diagram is constructed looking down at the equatorial plane (the blue plane of Fig 4)
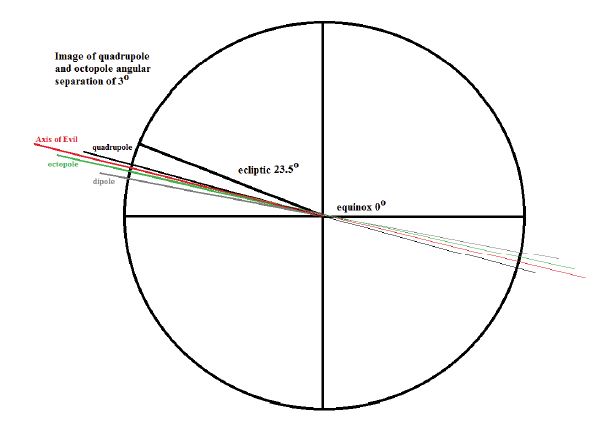
Fig 3: One of Sungenis’s diagrams that he claims is based on Fig 2. But since we see the ecliptic plane edge-on we must be looking at a plane orthogonal to the equatorial and ecliptic planes. One can only represent declinations in this view.
Sungenis claims that his diagram immediately below Longo’s (Fig 3) is based on what he refers to as Longo’s “pie chart”. Of course Longo’s diagram is not a pie chart, which is an entirely different sort of diagram, but, more importantly, we can immediately see by his inclusion of the ecliptic that it isn’t even a diagram looking down at the equatorial plane as Longo’s is – it is rotated by 90° with respect to Longo’s. The ecliptic plane is seen edge-on, so Sungenis’s diagram represents a plane normal to both the equatorial and ecliptic planes. He labels the horizontal axis which represents the equatorial plane with the symbol “equinox 0°”, but the equinox cannot possibly lie on this axis, as, by definition, the equinox is in the direction of the line where the ecliptic and equatorial planes intersect and therefore perpendicular to the plane of the paper in this diagram. If Sungenis wishes to plot directions on Fig 3 he must extract only the declination components as the right ascension components cannot be represented.
Of course, all of this is lost on Sungenis, who, in his confusion, proceeds to plot the total angles between various features, on his diagram where only declination can properly be represented. This leads him to make nonsensical statements such as:
We see that the CMB multipoles are between the equinox and the ecliptic…
This is foolish nonsense because the equinox lies in the ecliptic plane, by definition, and so there is no “between” them – yet another elementary blunder from scientific ignorance. We can ignore the rest of his analysis and his claims in this section as they are based on this gross misunderstanding of astronomical geometry, making the angles that he quotes spurious.
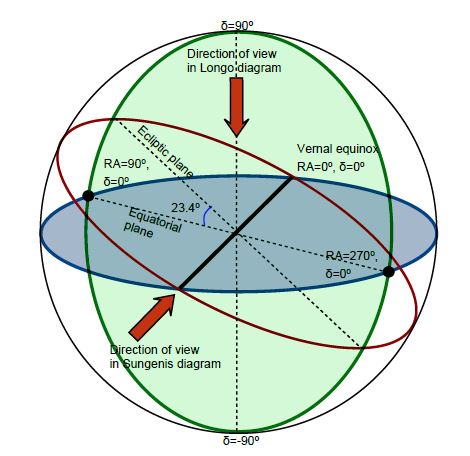 Fig 4: Longo’s diagram is looking down at the equatorial plane (blue) whereas Sungenis is looking at the equatorial and ecliptic planes edge-on and on to the green plane. The respective directions of view are shown by red arrows.
Fig 4: Longo’s diagram is looking down at the equatorial plane (blue) whereas Sungenis is looking at the equatorial and ecliptic planes edge-on and on to the green plane. The respective directions of view are shown by red arrows.
Sungenis finishes this shambolic analysis with calculations that are pure numerology – averaging separately the right ascensions and the declinations of the dipole, a selection of the low multipoles (but not the third octopole area vector), the Longo spiral galaxy spin axis and even the North Galactic pole to arrive at a direction near the equinox. Within this numerology, he repeats his hopeless misunderstanding by talking about things lying between the equinox and the ecliptic, when, by definition, the equinox lies on the ecliptic plane. Is it possible that he is conflating the equator with the equinox? Given Sungenis’s incompetence, any error, no matter how elementary and absurd, is possible.
Robert Sungenis has demonstrated again and again throughout this controversy that he is mathematically and scientifically incompetent. That incompetence is apparent most recently in his two mutually exclusive but equally wrong attempts to answer the CMB Challenge. Time and again he shows, in objective ways, that he quite literally does not know what he’s talking about.
Sungenis and his geocentric followers will likely dismiss all of this detailed rebuttal as merely a matter of differing interpretation or, even more likely, will ignore the concrete demonstration of his errors and attempt to console their loyal followers by obfuscation and misdirection.
But make no mistake, we are talking about mathematics here – there are right and wrong answers and Sungenis repeatedly gets the answers wrong. Based on the specified data, the CMB misalignments are exactly as I stated in my original article. What is more, the CMB features do not “point like an arrow . . . directly to the Earth”, “point directly to the Earth as the center”, “show that the whole Universe is centered on the Earth”, or support any of the other extravagant claims of the geocentrists (see the original “CMB Alignment Challenge” and also “Yes, the CMB Misalignments Are a Problem for the New Geocentrists”).
Sungenis has now failed the CMB Alignment Challenge, not once but twice, and in doing so has further demonstrated his mathematical and scientific incompetence.
Appendix: co-ordinate transformations
Directions in a celestial co-ordinate system can be transformed to a different co-ordinate system by spherical trigonometry using the spherical cosine and sine rules, or by the use of rotation matrices. Both approaches are extensively covered in textbooks of mathematics, astronomy and geodesy – see Astrophysical Formulae: Space, Time, Matter and Cosmology, Vol II by Kenneth Lang or Practical Astronomy by Peter Duffett-Smith or Fundamentals of Celestial Mechanics Second Edition by J. M. A. Danby, or on-line for example here, here and here. I will briefly set out the fundamentals of the rotation matrix approach.
If a direction in co-ordinate system O is given by a vector r, then the same direction in co-ordinate system O’ is given by:
![]() where R is the rotation matrix, and the vector matrix of a vector with co-ordinates (α, δ) is:
where R is the rotation matrix, and the vector matrix of a vector with co-ordinates (α, δ) is:
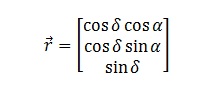 Any rotation R can be represented by a series of rotations about the axes x, y and z:
Any rotation R can be represented by a series of rotations about the axes x, y and z:
Equatorial to ecliptic and vice versa
Transforming equatorial to ecliptic co-ordinates is simple, since both co-ordinate systems have the same primary direction towards the vernal equinox, so the transformation is a single rotation by ε, the obliquity of the ecliptic about the ecliptic-equatorial nodal line. The rotation matrix is therefore:
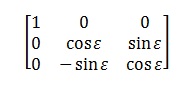 and for converting from ecliptic to equatorial co-ordinates it’s:
and for converting from ecliptic to equatorial co-ordinates it’s:
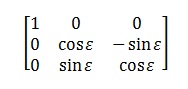 So the co-ordinates (λ, β) in ecliptic co-ordinates of a vector given in equatorial co-ordinates (α, δ) are:
So the co-ordinates (λ, β) in ecliptic co-ordinates of a vector given in equatorial co-ordinates (α, δ) are:
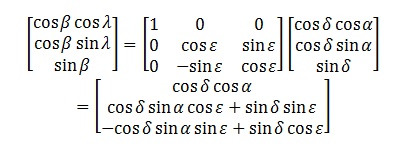 So cos β cos λ = cos δ cos α
So cos β cos λ = cos δ cos α
and cos β sin λ = cos δ sin α cos ε + sin δ sin ε
giving by division of these matrix elements:
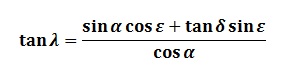 And the third matrix element gives
And the third matrix element gives
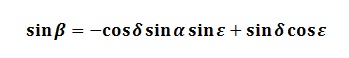 These two equations can be used for converting from equatorial to ecliptic coordinates and the equations for converting ecliptic to equatorial co-ordinates can be derived in a similar way using the appropriate rotation matrix. For the first expression, one has to be careful to establish the correct quadrant, as the arctan function is ambiguous.
These two equations can be used for converting from equatorial to ecliptic coordinates and the equations for converting ecliptic to equatorial co-ordinates can be derived in a similar way using the appropriate rotation matrix. For the first expression, one has to be careful to establish the correct quadrant, as the arctan function is ambiguous.
Ecliptic/equatorial to galactic and vice versa
The galactic co-ordinate system was defined by the International Astronomical Union in the B1950 epoch by three numbers:
- the right ascension in B1950 equatorial co-ordinates of the azimuth of the north galactic pole’s tilt = 192.25°
- the tilt of the galactic plane with respect to the equatorial plane which is 62.6° giving the declination of the pole in B1950 equatorial co-ordinates = +27.4°
- the angle of the galactic zero of longitude with respect to the north celestial pole = 123°
The ascending node of the galactic plane lies at (α=192.25° + 90°, δ = 0°) in equatorial co-ordinates and at (l=123° – 90°, b=0°) in galactic co-ordinates. The transformation consists of three rotations:
- A rotation Φ of 192.25° + 90° = 282.25° about the celestial polar axis to put the zero of longitude at the ascending galactic node, (rotation about the z-axis)
- A rotation θ of 62.6° about the intersection of the fundamental planes, the nodal line (rotation about the x-axis) to tilt the fundamental galactic plane with respect to the equatorial plane
- A rotation of 123° – 90° = 33° about the galactic polar axis to set the primary direction of the galactic system towards the galactic centre in longitude (rotation about the z’-axis)
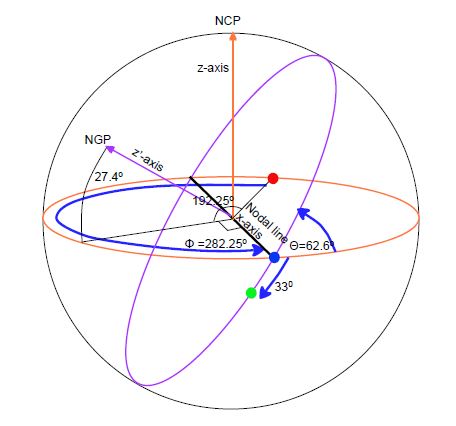 Fig 5: Transforming equatorial to galactic co-ordinates. The equatorial plane and polar axis are orange. The galactic plane and polar axis are purple. NCP is the north celestial pole and NGP is the north galactic pole. The red dot is the vernal equinox which is the primary direction of the equatorial co-ordinate system, the blue dot is the ascending node of the galactic plane and the green dot is the direction of the galactic centre which is the primary direction of the galactic co-ordinate system. The transformation rotations are indicated by blue arrows
Fig 5: Transforming equatorial to galactic co-ordinates. The equatorial plane and polar axis are orange. The galactic plane and polar axis are purple. NCP is the north celestial pole and NGP is the north galactic pole. The red dot is the vernal equinox which is the primary direction of the equatorial co-ordinate system, the blue dot is the ascending node of the galactic plane and the green dot is the direction of the galactic centre which is the primary direction of the galactic co-ordinate system. The transformation rotations are indicated by blue arrows
The transformation from equatorial co-ordinates (α, δ), to galactic co-ordinates (l, b) is therefore:
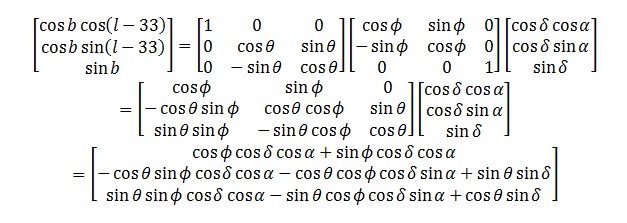 Therefore, rearranging, substituting for constant values and dividing the second element of the matrix by the first gives:
Therefore, rearranging, substituting for constant values and dividing the second element of the matrix by the first gives:
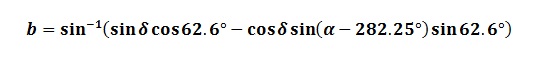 These two equations give the transformation from B1950 equatorial co-ordinates to galactic co-ordinates. The expressions for converting from galactic to B1950 equatorial co-ordinates are derived in a similar way with the appropriate rotation matrices. For the first expression, one has to be careful to establish the correct quadrant, as the arctan function is ambiguous.
These two equations give the transformation from B1950 equatorial co-ordinates to galactic co-ordinates. The expressions for converting from galactic to B1950 equatorial co-ordinates are derived in a similar way with the appropriate rotation matrices. For the first expression, one has to be careful to establish the correct quadrant, as the arctan function is ambiguous.
The transformation from ecliptic co-ordinates is done by first converting from ecliptic co-ordinates to B1950 equatorial co-ordinates and then applying the expressions above. When going from galactic to ecliptic co-ordinates, the first step is to transform to B1950 equatorial co-ordinates, and then to ecliptic co-ordinates.
If, one is working with a different equinox, such as J2000 as specified in the challenge, one has to be careful to precess to B1950 from the other epoch/equinox before converting to galactic co-ordinates and vice versa when going the other way. This correction is necessitated by the axial precession of the Earth’s polar axis with respect to the star field with a period of ~26,000 years.
This can be done by using appropriate rotation matrices or the simple approximate equations here:
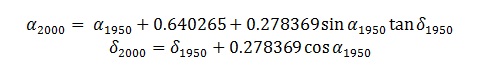 So the full process for going from galactic coordinates to ecliptic co-ordinates in the J2000 epoch is:
So the full process for going from galactic coordinates to ecliptic co-ordinates in the J2000 epoch is:
- Transform from galactic co-ordinates to the B1950 equatorial co-ordinates
- Precess these to J2000 equatorial co-ordinates
- Transform the J2000 equatorial co-ordinates to ecliptic co-ordinates using the J2000 epoch obliquity.
And that’s before we consider the small influences of stellar aberration, precession and nutation of date and the ellipticity of the Earth’s orbit. No wonder people use on-line tools for celestial co-ordinate transformations!
Nevertheless, the on-line tools use the expressions and rotation matrices that we have looked at in this appendix in order to do the calculation in the background, and it’s always good to understand what’s happening rather than just blindly entering data into an on-line tool and pressing the “convert” button.